Part1 常量定义

1.常值定义

MAX_NAME_LEN 最大姓名长度

MAX_CLASS_LEN 最大班级编号长度

MAX_ID_LEN 最大学号长度

MAX_SCORE_LEN 最大成绩长度

MAX_STACK_SIZE 最大栈空间

MAX_BUFFER_SIZE 缓冲区最大空间

MAX_STU_BUFFER_SIZE 学生实例缓冲区最大空间

2.常字符串定义

BANNER_WORD 欢迎使用的提示

FUNC1_WORD 功能1：输入学生姓名的提示

FUNC2_WORD 功能2：列出全部学生信息的提示

FUNC3_WORD 功能3：按成绩排名

FUNC4_WORD 功能4：按学号排名

FUNC5_WORD 功能5：计算平均分

FUNC6_WORD 功能6：统计成绩区间内人数

FUNC7_WORD 功能7：退出系统

INPUT1_WORD 功能1输入提示信息

INPUT11_WORD 功能1第一项提示信息

INPUT12_WORD 功能1第二项提示信息

INPUT13_WORD 功能1第三项提示信息

INPUT14_WORD 功能1第四项提示信息

CHOICE_ERROR_MSG 输入选项不合法的提示信息

3.地址表定义

TABLE_HINT_STRING 用于将提示信息传递到显示函数中

TABLE_POINTERS 用于向子程序中传递指针寄存器

TABLE_CMP_STRING 用于比较两字符串时传递参数

4.系统调用定义

CR 定义回车

LF 定义换行

IN_AND_OUT 接收输入并回显

DISP_CHAR 显示一个字符

DISP_STR 显示一个字符串

RETURN 返回操作系统

STR_TO_BUF 从键盘读取字符串并写入缓冲区

Part2 数据结构及定义

1. Student

类型:Struc

作用:描述一个学生的结构体，包含学生姓名，班级，学号，成绩

Part3 变量及其定义

1.OPTION1：

用户在第一个菜单界面下输入的选项

2.BUFFER

输入字符串的缓冲区

包含缓冲区最大长度、缓冲区实际容量及缓冲区存放的字符串

3.STU_NAME_TMP

临时存放输入的学生姓名

4.STU_ID_TMP

临时存放输入的学生学号

5.STU_SCORE_TMP

临时存放输入的学生成绩

6.STU_CLASS_TMP

临时存放输入的学生班级

Part4 函数定义

1.PUTS

作用：在屏幕上显示一行字符串并换行

参数：

TABLE_HINT_STRING

返回值：无

2.DISPLAY_MENU

作用：在屏幕上显示菜单 参数：

TABLE_HINT_STRING

返回值：无

3.CHOICE_INPUT

作用：接受用户输入的选项，并判断是否是合法选项

参数：无

返回值：无

4.INPUT

作用：供用户输入学生信息

参数：无

返回值：无

5.ADD_INTO_BUF

作用：将临时存储学生信息的结构体加入到全局的学生缓冲区中

参数：Student

返回值：无

6.PUTS

作用：在屏幕上显示一行字符串

参数：

TABLE_HINT_STRING

返回值：无

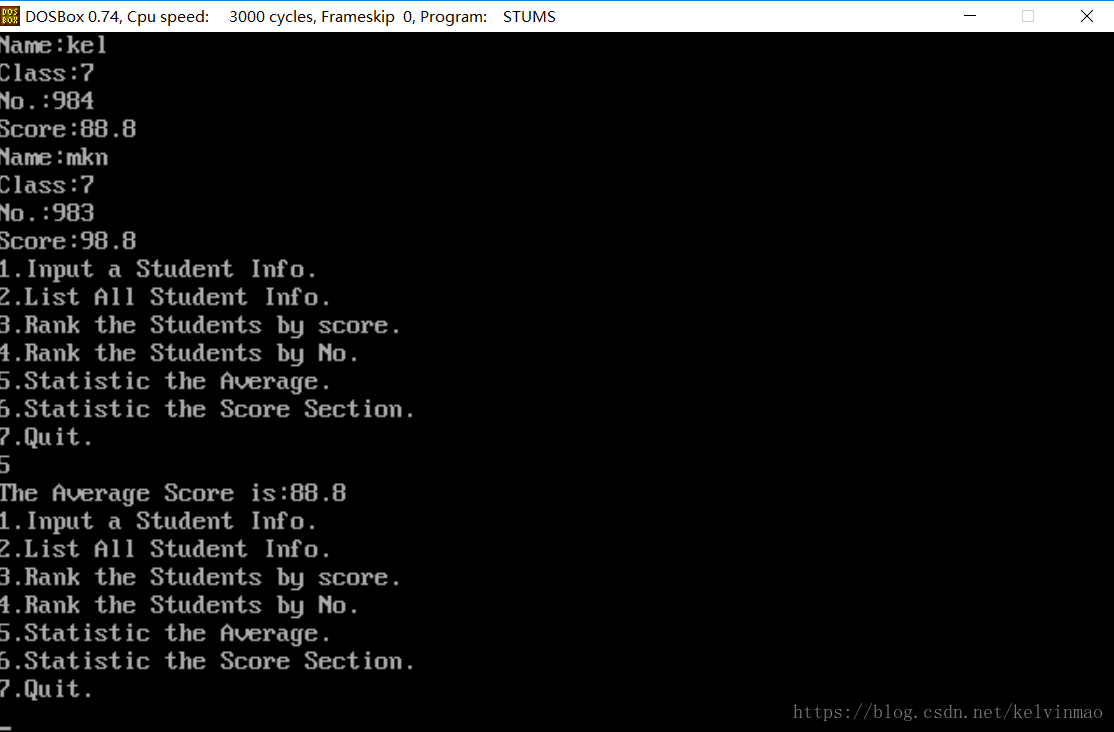
运行截图

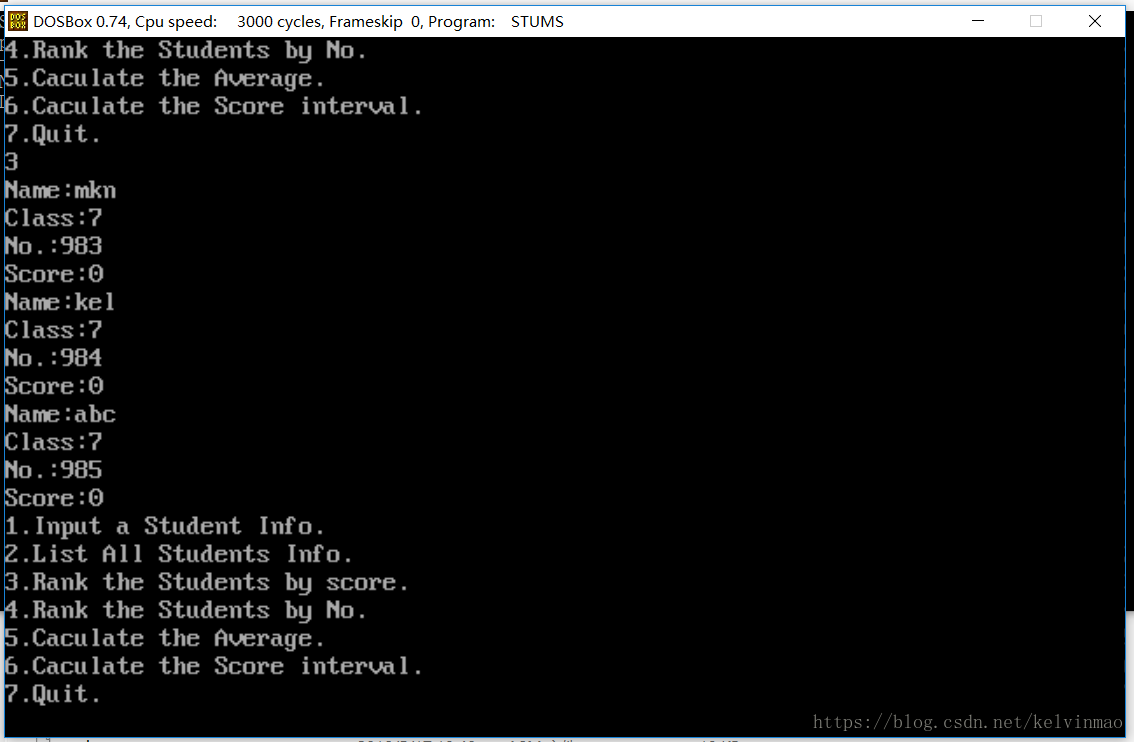
输入学生信息

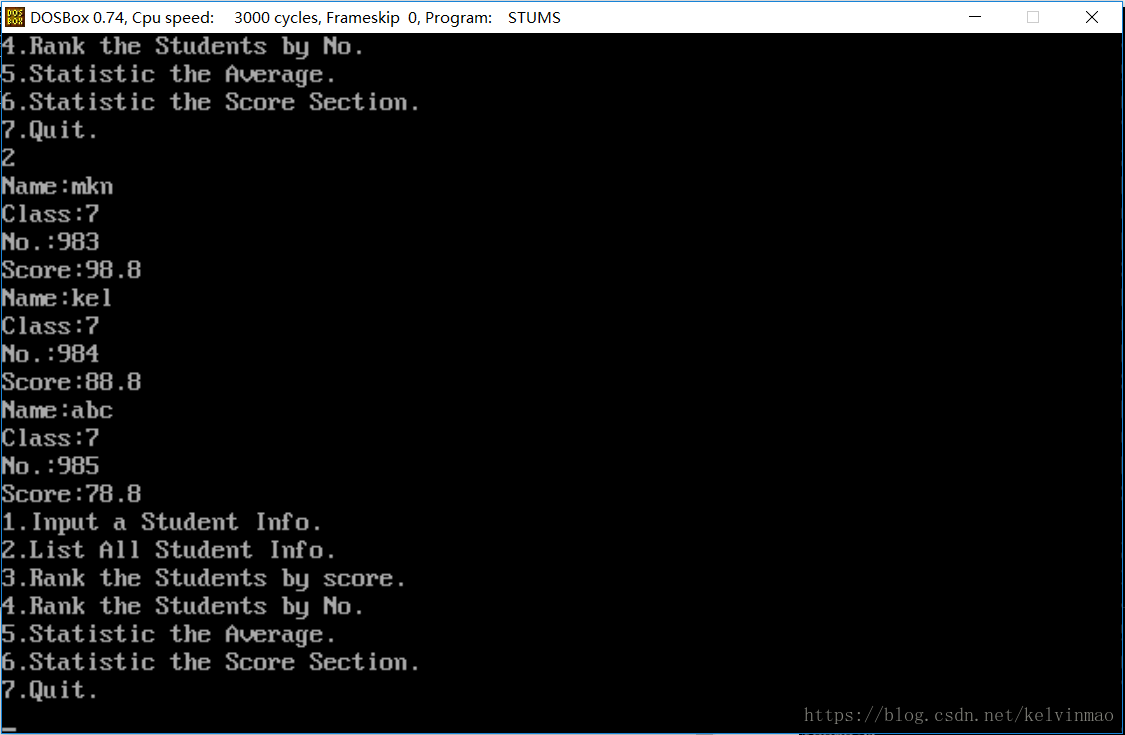
列出所有学生

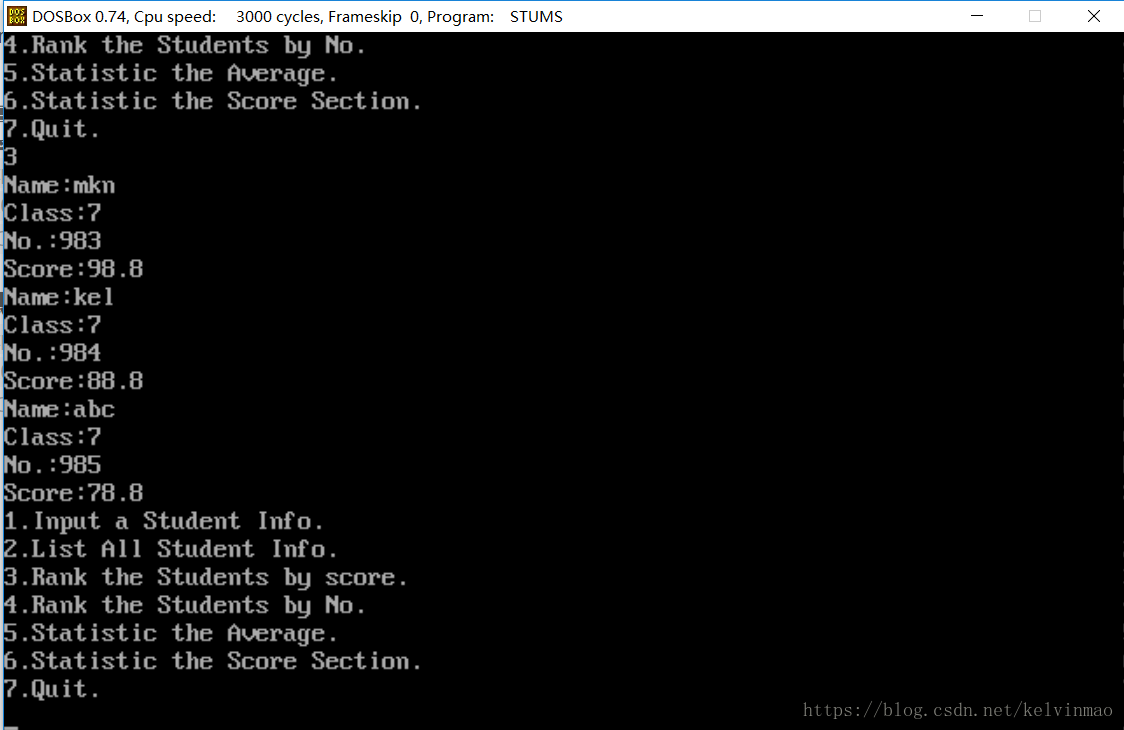
按成绩排名

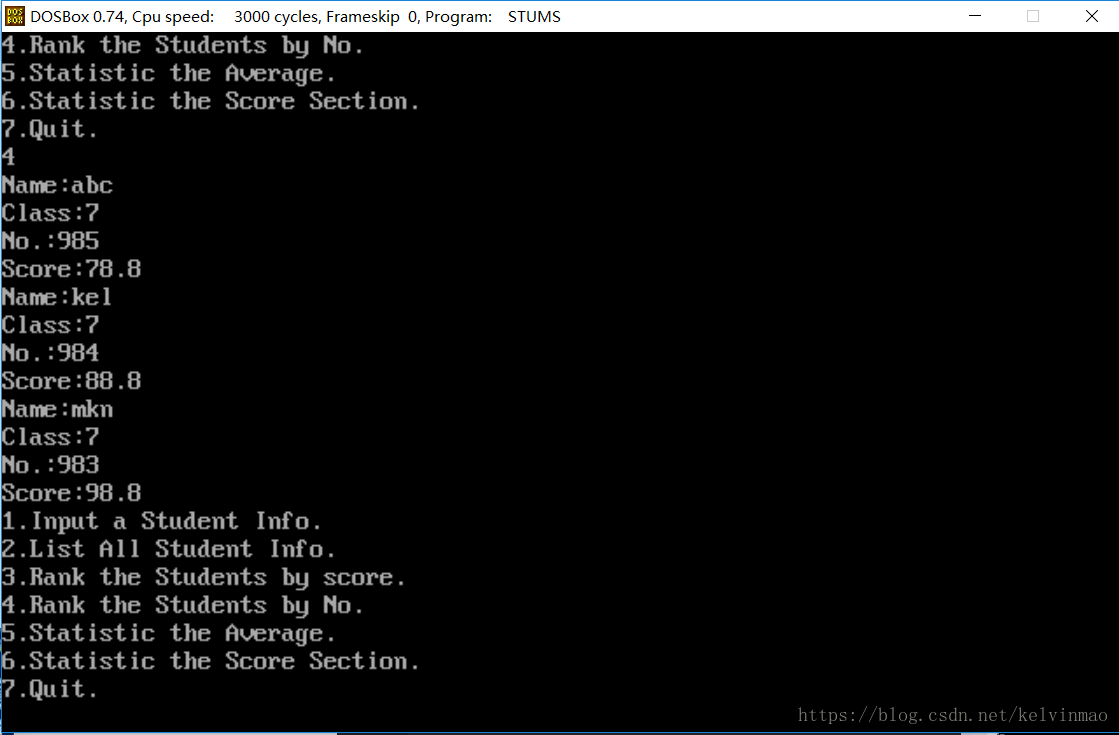
按学号排名

计算平均分

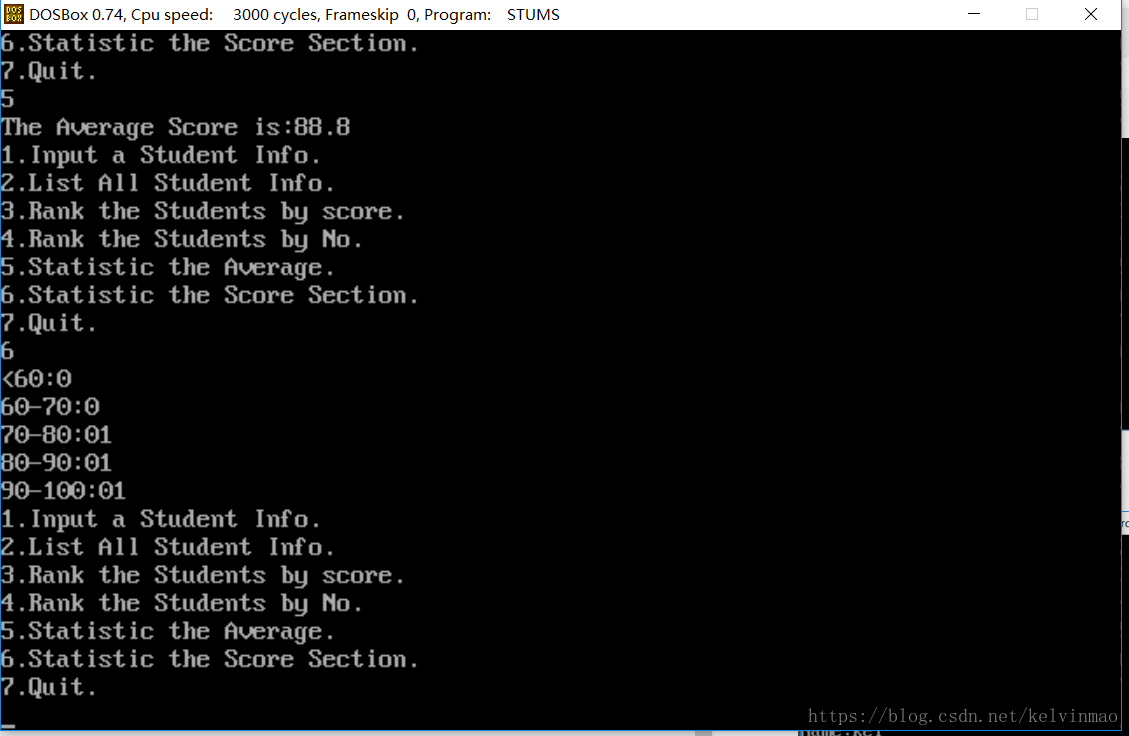
划分成绩区间

编写过程中的问题

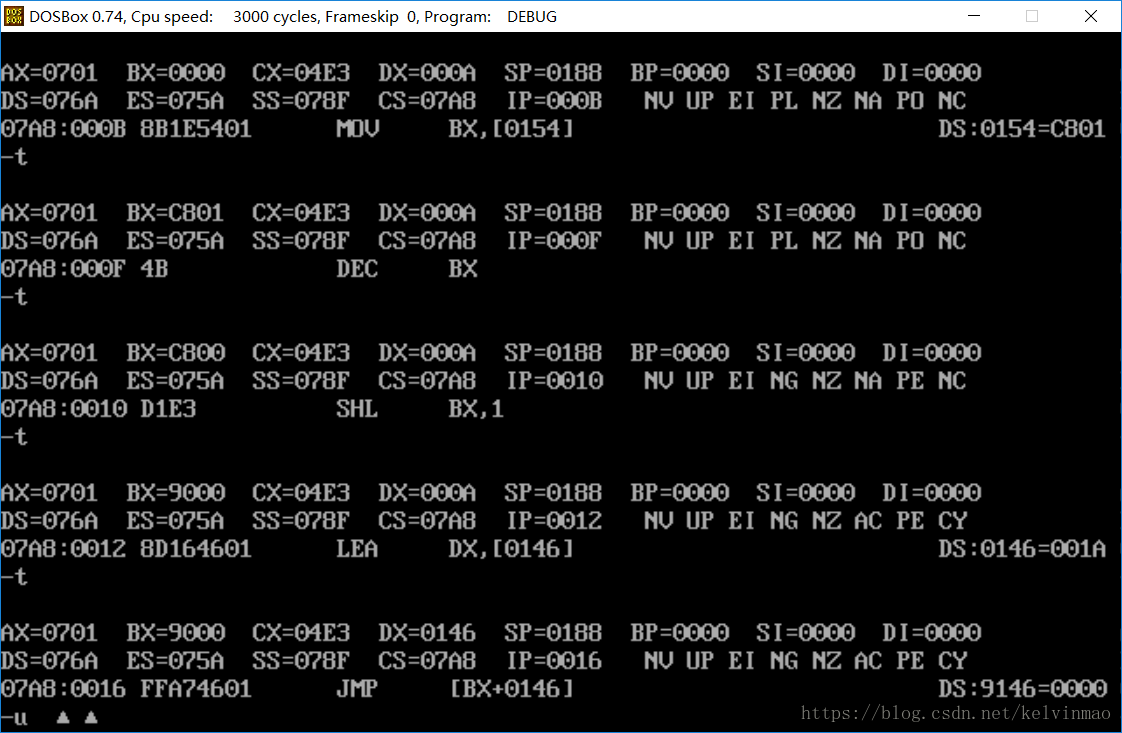
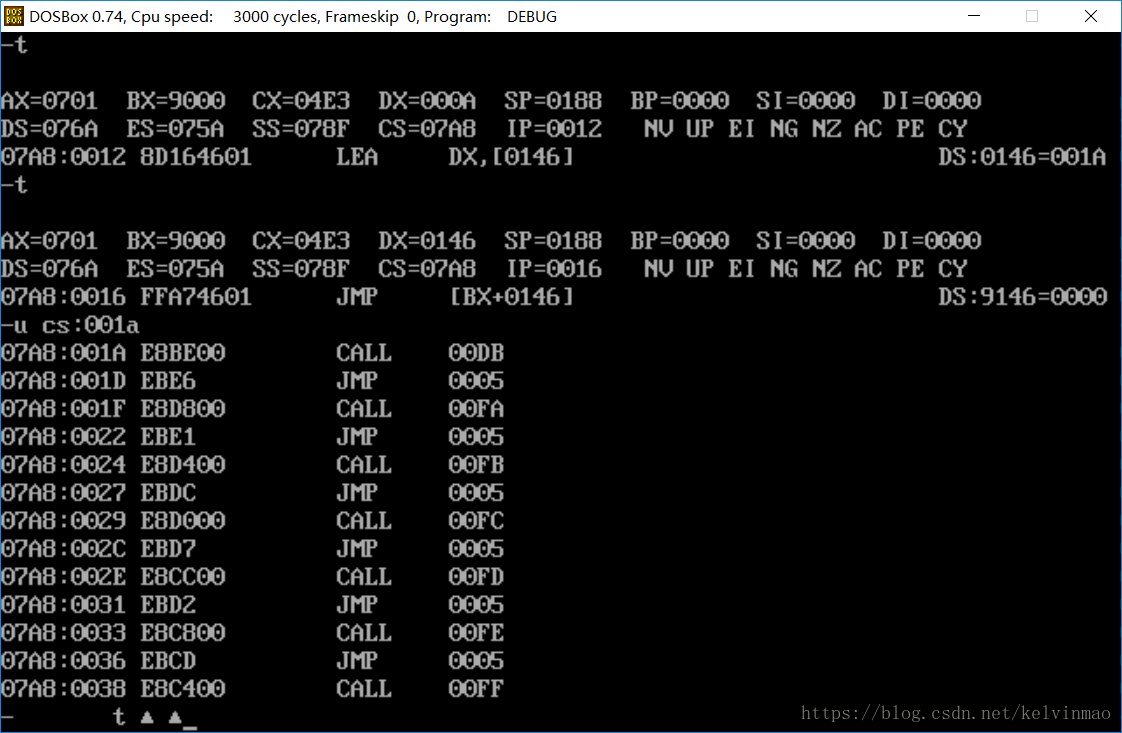
1.跳转表

跳转表没有跳到case，跳到了cs:0000，输入选项之后不断重新显示菜单

跟踪发现跳转表地址应该是DS:0146，但最后跳转表的地址变为DS:9146，发现是BX寄存器（BH）的值造成了影响，于是将BH置为0，问题解决

为什么会有这样一个工具？

<p>
    之前是有一位学长写了JS版和Python版的评教脚本，不过自从教务系统加了验证码后就废弃无人维护了。
    
    众所周知，北邮的教学评估总是安排在期中期末复习周，然而，凡是使用过教学评估界面的同学都能理解在评教界面上找到选项并点击有多困难。
    
    <br>更可怕的是,每个老师通常都会有7~8个选项，一个一个点下来眼睛都要瞎了。<br>
    鉴于此，为了解决这个问题，我写了这样一个“糙猛快”的脚本，来帮助大家一键评教。
</p>

我该如何使用它？

仓库地址： 环境配置： Python 3.6 依赖模块： Beautifulsoup Request urllib lxml 上述模块通过pip安装即可（pip install + 模块名） 安装完毕，确认自己处于校园网环境下并能正常打开教务系统后，更改param中的参数“zjh”和"mm"为自己的教务系统登录账号和密码即可。 运行之后，会提示输入验证码，验证码默认保存在D盘，需要改的请自己更改"dest_url"参数至别的路径。 验证码输入后，如果未抛出任何异常，应该可以在console中看到一闪而过的课程列表以及最希望看到的评估成功。 至此，评教就已经顺利完成了。

写在最后

1.因为是突发奇想写的，所以可能会存在一些问题，使用时遇到问题记得先问问谷歌

2.还是由于突发奇想写的，界面十分简陋，其实验证码可以通过OCR解决的，不过懒得折腾，有想法的同学自己折腾一下吧。最好能部署成云服务的形式，使用更方便，用户也就不用配置各种依赖了。

72.Edit distance

Description

Given two words word1 and word2, find the minimum number of steps required to convert word1 to word2. (each operation is counted as 1 step.)

You have the following 3 operations permitted on a word:

a) Insert a character

b) Delete a character

c) Replace a character

这道题要求求解两个字符串之间的编辑距离，也就是通过增删改，最少多少次才能把一个字符串转换为另一个字符串。

对于这种对字符串进行修改还要求极值的题目，一般使用动态规划来解决，需要解决的是动态规划过程中的状态方程。

依然用i，j两个变量代表当前需要判断的字符串长度，如果两个字符串i-1和j-1位置上的字符相同，则不需要进行修改，即dp[i][j]=dp[i-1][j-1]

如果不匹配，则需要考虑增删改三个操作分别的代价。

考虑增加，如果需要在前一个字符串第i位增加一个字符串，使其与第二个字符串相同，则需要的步数是：dp[i][j-1]+1，也就是取决于将长为i的字符串与长为j-1的字符串相匹配的修改次数+一次增加

考虑删除，如果需要删除第i位的字符使其与第二个字符串相同，则需要的步数是：dp[i-1][j]+1，与增加同理

考虑替代，如果需要将第i位的字符替代，使其与长为j的字符串相同，只需要考虑前i-1，j-1的修改次数+1即可

之后选出代价最小的方式即可。

状态方程梳理清楚后，就很容易写出代码了，需要注意的是在对第一行第一列进行初始化时，略有不同

代码如下：

class Solution {
    public int minDistance(String word1, String word2) {
        int [][]dp=new int[word1.length()+1][word2.length()+1];
        for(int i=0;i<=word1.length();++i){
            for(int j=0;j<= word2.length();++j){
                if(i==0||j==0){
                    dp[i][j]=i+j;
                }
                else{
                    if(word1.charAt(i-1)==word2.charAt(j-1))
                        dp[i][j]=dp[i-1][j-1];
                    else{
                        int replace=dp[i-1][j-1];
                        int delete=dp[i-1][j];
                        int insert=dp[i][j-1];
                        dp[i][j]=Math.min(Math.min(replace,delete),insert);
                        dp[i][j]++;
                    }
                }
            }
        }
        return dp[word1.length()][word2.length()];
    }
}

583.Delete Operation for Two Strings

Description

Given two words word1 and word2, find the minimum number of steps required to make word1 and word2 the same, where in each step you can delete one character in either string.

Example 1:

Input: "sea", "eat"
Output: 2
Explanation: You need one step to make "sea" to "ea" and another step to make "eat" to "ea".

Note:

The length of given words won’t exceed 500.

Characters in given words can only be lower-case letters.

这是一道非常有趣的题目，间接考察最长公共子序列的求解

最长公共子序列和之前做过的最长公共子串略有不同，子串要求字母必须相连，而子序列则没有这个要求，比如：

cnblog和belong，最长公共子序列是blog，而最长公共子串是lo

结合公式，所需的删除操作的次数=word1的长度+word2的长度-2*最长公共子序列的长度。我们首先需要求解除吧最长公共子序列的长度。

最简单的方法当然是使用递归，如果[0,i],[0,j]最后一个字符相同，则比较[0,i-1],[0,j-1]的最后一个字符，若不相同，则删去第i个或第j个字符后，返回长度更长的子序列，代码如下：

public class Solution {
    public int minDistance(String s1, String s2) {
        return s1.length() + s2.length() - 2 * lcs(s1, s2, s1.length(), s2.length());
    }
    public int lcs(String s1, String s2, int m, int n) {
        if (m == 0 || n == 0)
            return 0;
        if (s1.charAt(m - 1) == s2.charAt(n - 1))
            return 1 + lcs(s1, s2, m - 1, n - 1);
        else
            return Math.max(lcs(s1, s2, m, n - 1), lcs(s1, s2, m - 1, n));
    }
}

但很不幸，这样得到的结果是TLE，所以还是要借助动态规划算法求解此类问题。

如果使用动态规划求解最长公共子序列，那么假设[0,i],[0,j]的最后一个字符匹配，则LCS的长度取决于第i-1和j-1个字符；如果不匹配，则需要进行错位比较，也就是说，LCS的长度取决于[i-1]或[j-1]（取较长的一个），代码如下：

class Solution {
    public int minDistance(String word1, String word2) {
        int dp[][]=new int[word1.length()+1][word2.length()+1];
        for(int i=0;i<word1.length()+1;++i){
            for(int j=0;j<word2.length()+1;++j){
                if(i==0||j==0)
                    continue;
                if(word1.charAt(i-1)==word2.charAt(j-1))
                    dp[i][j]=dp[i-1][j-1]+1;
                else
                    dp[i][j]=Math.max(dp[i-1][j],dp[i][j-1]);
            }
        }
        return word1.length()+word2.length()-2*dp[word1.length()][word2.length()];
    }
}

这个算法的原理可见动图 https://leetcode.com/problems/delete-operation-for-two-strings/solution/

当然，也可以直接借助动态规划求解修改次数，思路和上面的方法差不多，用dp[i][j]表示要将两字符串删除至相等时的删除次数。代码如下：

class Solution {   
    public int minDistance(String word1, String word2){
        int dp[][]=new int[word1.length()+1][word2.length()+1];
        for(int i=0;i<=word1.length();++i){
            for(int j=0;j<=word2.length();++j){
                if(i==0||j==0)
                    dp[i][j]=i+j;
                else if(word1.charAt(i-1)==word2.charAt(j-1))
                    dp[i][j]=dp[i-1][j-1];
                else
                    dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+1;
            }
        }
        return dp[word1.length()][word2.length()];
    }
}

521. Longest Uncommon Subsequence I

Description

Given a group of two strings, you need to find the longest uncommon subsequence of this group of two strings. The longest uncommon subsequence is defined as the longest subsequence of one of these strings and this subsequence should not be any subsequence of the other strings.

A subsequence is a sequence that can be derived from one sequence by deleting some characters without changing the order of the remaining elements. Trivially, any string is a subsequence of itself and an empty string is a subsequence of any string.

The input will be two strings, and the output needs to be the length of the longest uncommon subsequence. If the longest uncommon subsequence doesn’t exist, return -1.

Example 1:

Input: "aba", "cdc"
Output: 3
Explanation: The longest uncommon subsequence is "aba" (or "cdc"), 
because "aba" is a subsequence of "aba", 
but not a subsequence of any other strings in the group of two strings. 

Note:

1.Both strings’ lengths will not exceed 100.

2.Only letters from a ~ z will appear in input strings.

这道题要求返回两个字符串的最长非平凡子序列，在题目的描述中，对最长非平凡子序列给出了如下的定义：

最长非平凡子序列是指：某个字符串的子字符串，不是另一个字符串的子串。

具体的例子见题干中给出的Example。

这种题很适合采用“测试驱动开发”的原则，给出下列测试用例：

1.“aba”,”cdc”,由于两者之间互不为子串，所以返回两者之中的最长字符串的长度即可

2.“aba”,”babac”,由于aba是后者的子串，但后者却不是前者的子串，所以返回较长的即可

3.两者中有一个为空串，由于题目说明空串是任何字符串的子串，所以依然返回较长的即可

4.两字符串相等，如“aaa”,”aaa”,找不到某一个子串同时不为另一个字符串的子串，所以返回-1

总结一下上述情况，其实就是两个字符串不相等时返回较长的，相等时返回-1，代码如下:

public class Solution {
    public int findLUSlength(String a, String b) {
        if(!b.contains(a)&&!a.contains(b))
        	return Math.max(a.length(), b.length());
        if(a.contains(b)&&b.contains(a))
        	return -1;
        if(a.contains(b)||b.contains(a))
        	return Math.max(a.length(), b.length());
        if(("".equals(a)&&!"".equals(b))||(!"".equals(a)&&"".equals(b)))
        	return Math.max(a.length(), b.length());
        else
        	return 0;
    }
}

one-line版本的如下：

public class Solution {
    public int findLUSlength(String a, String b) {
        return a.equals(b)? -1 : Math.max(a.length(),b.length());
    }
}