204. Count Primes

Description:

Count the number of prime numbers less than a non-negative number, n.

给出一个非负整数n，要求返回比n小的素数的个数

看起来非常容易，只需要写一个判断素数的函数isPrime()函数，然后对从2~n的数字进行判断就可以了，但是如果有这么简单，这道题也就不会作为面试题进行考察了。因为这个O(n^2)的算法会被OJ判为超时，即使你已经考虑了循环条件是:i<sqrt(n),而不是i<n。

考虑到统计个数的复杂度基本没有降低的希望，所以我们在判断素数这个函数上做优化。

因为之前学过的判断素数的算法只是在循环条件上做优化，所以最多也只能将时间复杂度降低到O(n^1.5),所以我们需要一种新的判断素数的思路。

我们要AC这道题，就必须使用sieve of Eratosthenes算法，中文名是埃拉托斯特尼筛法，不要被它的名字吓到，原理很简单，就是从2开始，将每个素数的各个倍数，标记成合数。下面这张图可以帮助理解

按步骤对算法的运行状况进行分析:

首先列出2以后的所有序列： 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 标出序列中的第一个质数，也就是2，序列变成： 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 将剩下序列中，划掉2的倍数，序列变成： 2 3 5 7 9 11 13 15 17 19 21 23 25 如果现在这个序列中最大数小于最后一个标出的素数的平方，那么剩下的序列中所有的数都是质数，否则回到第二步。

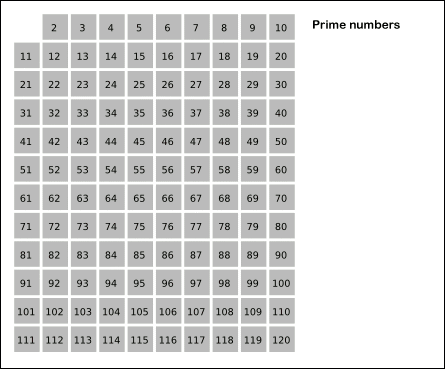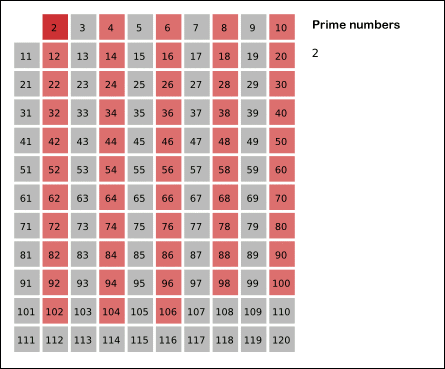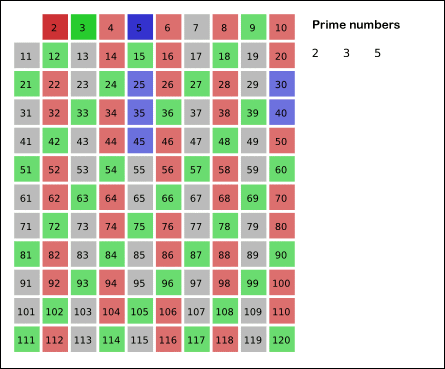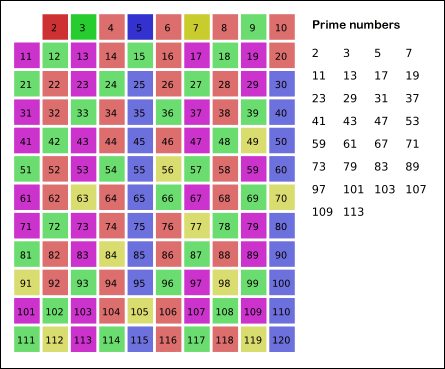
本例中，因为25大于2的平方，我们返回第二步： 剩下的序列中第一个质数是3，将主序列中3的倍数划出，主序列变成： 2 4 5 7 8 10 11 13 14 16 17 19 20 22 23 25 我们得到的质数有：2，3 25仍然大于3的平方，所以我们还要返回第二步： 现在序列中第一个质数是5，同样将序列中5的倍数划出，主序列成了： 2 3 5 7 11 13 17 19 23。 我们得到的质数有：2 3 5 。 因为25等于5的平方，跳出循环. 结论：去掉红色的数字，2到25之间的质数是：2 3 5 7 11 13 17 19 23。

class Solution {
public:
    int countPrimes(int n) {
        int count=0;
        bool isprime[n];
        for(int i=0;i<n;i++)
            isprime[i]=true;
        for(int i=2;i<sqrt(n);i++){
            if(isprime[i]){
                for(int j=2;j*i<n;j++)
                    isprime[j*i]=false;
            }
        }
        for(int i=2;i<n;i++){
            if(isprime[i]==true)
                count++;
        }
        return count;
    }
};

这个算法的时间复杂度为 O(n log log n)，数学上的证明请见维基百科(太复杂了)，由于申请额外空间，所以空间复杂度为O(n)